Towards the One-Point Function for the XXZ Spin-1/2 Chain on the Ring
Published:
Some observables from the XXZ spin-1/2 chain have shown KPZ behavior, but it is not entirely clear if the model lies within the KPZ universality class. Of particular interest for us is the one-point function, for which we aim to get an exact expression that is amenable to asymptotic analysis. This content and informal discussion is based on joint work with Axel Saenz Rodriguez.
XXZ on the ring
In previous posts (1,2) I introduced the XXZ spin-1/2 chain (aka the Heisenberg-Ising spin chain). The Hamiltonian for this model reads as follows
\[\begin{equation} \mathcal{H} = \sum_{i=1}^N S_i^x S_{i+1}^x + S_i^y S_{i+1}^y + \Delta(S_i^z S_{i+1}^z - 1/2) \end{equation}\]where the \(S_i^\alpha\) are the quantum spin operators
\[\begin{equation} S_i^\alpha = Id \otimes Id \otimes \cdots \otimes \sigma^\alpha \otimes Id \cdots \otimes Id \end{equation}\]and \(\sigma^\alpha\) are the 2x2 Pauli matrices. We are working with the XXZ chain on the ring (periodic 1D lattice) of length \(L\), so we identify the \(L+1\)‘th site with the first site, \(S_{L+1}^\alpha = S_1^\alpha\). The dynamics of the model are governed by the Schrodinger equation
\[\begin{equation} \frac{d}{dt} |\Psi(t)\rangle = \mathcal{H} |\Psi(t)\rangle \end{equation}\]where \(|\Psi(t)\rangle\) is an element of the Hilbert space \(\mathbb{H}\) containing the spin
configurations with a fixed number of down-spins and up-spins. That is, \(\mathbb{H}\subset \mathbb{V}_L = \mathbb{V}^{\otimes L}\) with \(\mathbb{V}=\mathrm{Span}\{|\uparrow\rangle, |\downarrow\rangle\}\). Our aim is have a complete spectral decomposition of the Hamiltonian \(\mathcal{H}\). That is, we want eigenvectors, \(|\Psi(t)\rangle\), of \(\mathcal{H}\) such that
with \(E\) the respective eigenvalue. Via the coordinate Bethe ansatz, we can construct eigenvectors with the change of coordinates
\[\begin{equation} |\xi\rangle = |\xi_1,\ldots,\xi_N \rangle = \sum_{x\in\mathcal{X}} u(\xi,x) |x\rangle \end{equation}\]where \(\mathcal{X}=\{(x_1 < \cdots < x_N) \mid x_i \in \mathbb{Z} / L \mathbb{Z} \}\) is the configuration space with the \(x_i\)‘th entry denoting the location of the \(i\)‘th up-spin, and we denote the corresponding eigenvalues \(E(\xi)\). Due to the periodic boundary conditions of the ring, the Bethe coordinates must satisfy a system of algebraic equations which we call the Bethe equations 1. We will denote the set of all \(\xi\)’s (eigenvectors) which are solutions to the Bethe equations by \(\Xi\) (up to permutation of the entries \(\xi=(\xi_1,\ldots,\xi_N)\). A priori it is not clear that these are a complete basis for \(\mathbb{H}\). To do this we shall write a complete basis we do know, the set of indicator functions on configurations, in terms of the Bethe vectors. More specifically, we conjecture a function \(ell(x,\xi)\) such that
\[\begin{equation} |x\rangle = \sum_{\xi \in \Xi} \ell(x,\xi) |\xi\rangle \end{equation}\]which is equivalent to
\[\begin{equation} \mathbb{1}(x=y) = \sum_{\xi\in\Xi} \ell(y,\xi) u(\xi,x) \end{equation}\]since \(|x\rangle = \sum_{y\in \mathcal{X}}\mathbb{1}(x=y)|y\rangle\). Then for an initial configuration \(|y\rangle\), we can write the solution to the Schrodinger equation
\[\begin{equation} |\Psi(t)\rangle = \sum_{x\in\mathcal{X}}\left(\sum_{\xi\in\Xi}\ell(y,\xi)u(\xi,x) e^{-i t E(\xi)} \right) |x\rangle \end{equation}\]and by some assumptions we didn’t state and quantum mechanics yada yada (I did warn you about informality), the probability function for configurations reads
\[\begin{equation} \mathbb{P}(|\Psi(t)\rangle = |x\rangle) = \langle x \mid \Psi(t) \rangle \langle \Psi(t) \mid x \rangle = \left| \sum_{\xi\in\Xi}\ell(y,\xi)u(\xi,x)e^{-itE(\xi)}\right|^2. \end{equation}\]With this probability function, we can then compute the one-point function (i.e. the probability of finding an up-spin at a specific location) by summing the probability function over all states containing an up-spin at the indicated site. That is
\[\begin{equation} \rho(x,t) = \sum_{\vec{x}\in\mathcal{X}(x)}\mathbb{P}(|\Psi(t)\rangle = |\vec{x}\rangle). \end{equation}\]Now it’s possible to due the brute for computation with a computer. We have done this with our conjectured \(u\) and \(\ell\) functions2, which you can see an example of in the following plots for a ring of lenght 21, 2 up-spins, and \(\Delta=0.13\).

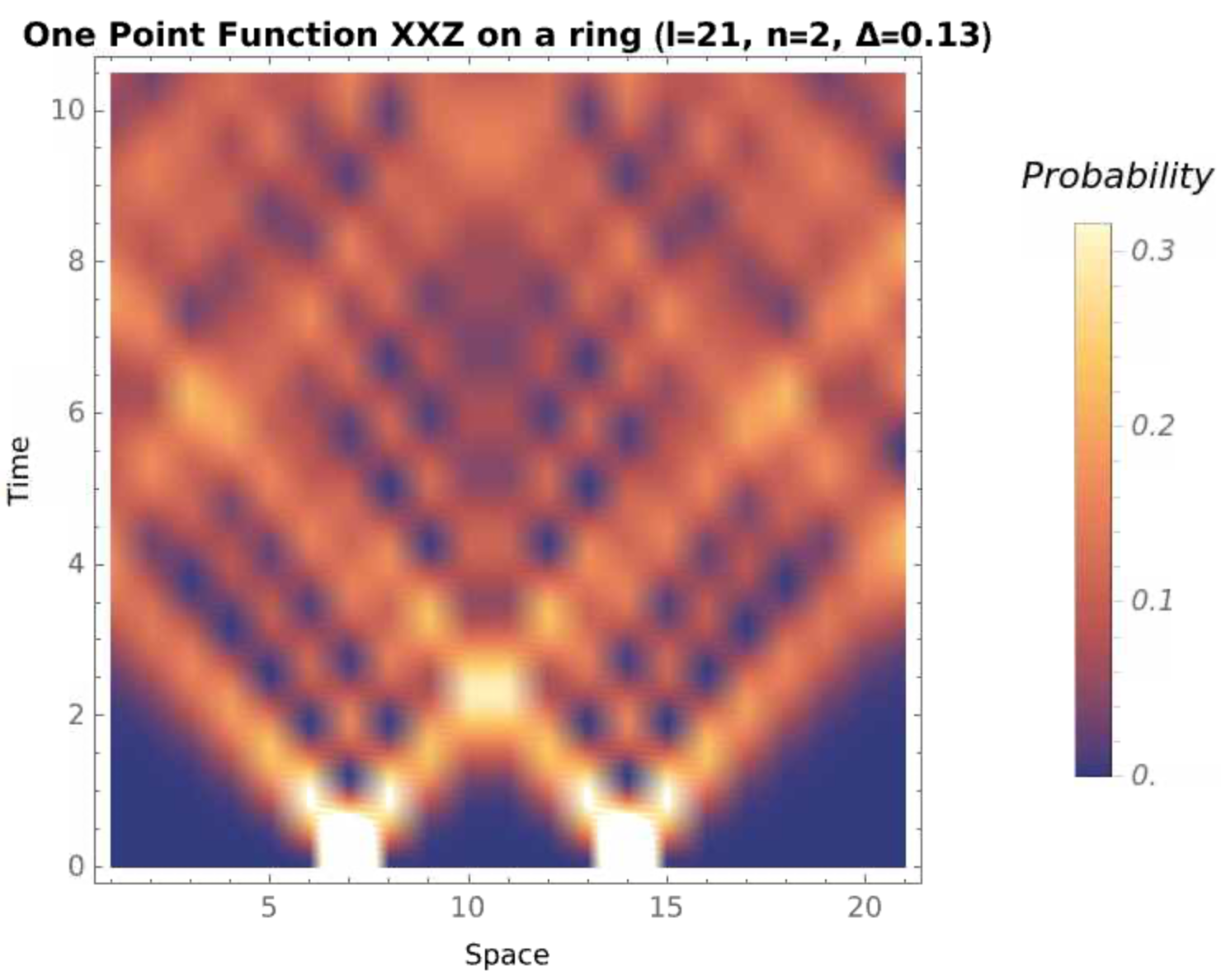
As it currently stands, however, this brute force computation with the current formula requires summing over \(L-1\) choose \(N-1\) configurations, and the current \(\ell\) and \(u\) functions sum over all permutations in \(S_N\) which adds \((N!)^4\) to the complexity due to the magnitude squared in the probability function. So brute force computation is very expensive if we want to increase the scale of our system (which we do). Hence, some serious simplification is needed, not just for improving simulation capability, but also if we want an expression that is amenable to asymptotic analysis. An expression in that sense is crucial to showing rigorous connections to the KPZ universality class (i.e. Tracy-Widom fluctuations).
The Bethe Equations are often avoided by considering the infinite line (\(\mathbb{Z}\)) instead of the ring. The reason for doing this is to avoid the issues of completeness of the Bethe ansatz. That is, proving that the Bethe vectors are a complete basis for the vector space \(\mathbb{H}\). ↩
I do not give the explicit functions since this work is still in-progress. ↩